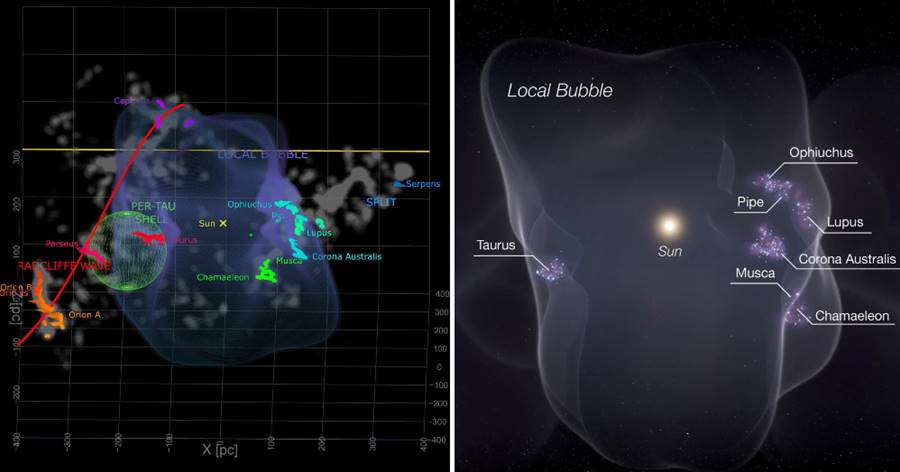
物體的被黑洞吸引的理論,來源于蘋果落地的故事,這個理論在1900年以前的確可以很好的解釋物體為什麼會落地。牛頓對于這個現象的解釋是力,即F=ma,力的大小與物體的質量和加速度有關,因此大家認為如果光子的質量為0,引力mg=0,光子壓根不受力,那麼為什麼會被黑洞「吸走」?

圖:黑洞吞噬光
關于這個問題,牛頓有牛頓的解釋方法,不過太為牽強,而愛因斯坦的解釋更為靠譜,就是比較抽象,我們先由淺入深說說牛頓的,再說說愛因斯斯坦的。
一、牛頓——萬有引力
引力加速度 逃逸速度 黑洞視界
二、愛因斯坦——廣義相對論
引力時空彎曲 一維到四維時空的螞蟻 簡述時空幾何 黑洞的曲率 光只是走了正確的路線
三、光子的質量與光子的宿命及宇宙的終結
引力加速度

圖:萬有引力公式
根據牛頓的萬有引力定律,我們可以知道引力的大小與兩個物體的質量和距離有關系。

圖:引力加速度
根據牛頓第二定律的重力大小F=mg,帶入萬有引力公式就可以得到引力的加速g。加速度的作用是決定物體往下掉的加速程度,或者說引力就不存在力的作用,它等效于加速與減速的作用。
如果一物體有一定的初始速度朝向地球發射,此時引力就像在踩剎車,例如火箭,隨著初速度減到0時,火箭就會在空中靜止。
之后加速g會繼續作用,如同踩油門,所以火箭會不斷加速下落。可見這個過程與質量半點關系都沒有。

圖:上升——停止——降落
不過距離r與g有關不能忽略,當火箭還在減速往外飛時,它離地球越來越遠,r越來越大。因為g與r的平方成反比,所以g會越來越小,即火箭飛得越高,減速的程度就越小。如果我們初始速度足夠大的話就克服地球的重力加速g,從而逃離地球的引力支配。

圖:扔標槍
通俗點來說,就是我們如果我們有足夠的力量朝天空扔出一個石頭,石頭是有可能飛出地球的(不考慮大氣因素),而這只和初始速度v有關,和物質無關,質量只是決定了物體要得到這個初速度需要用多大的力量。
多大的初始速度才能逃離地球?公式夠多了,這里就不贅述了,想了解網上一搜就有,這里直接給出:

圖:第二宇宙速度,也是火箭逃離地球控制的速度。
從逃逸速度公式看,我們發現跟要逃逸的物體質量還是沒有什麼關系。物體能否擺脫星球取決于星球的半徑和質量。

圖:初始速度小于逃逸速度(不考慮第一宇宙速度)
根據逃逸速度公式,如果有一個星球質量超級大,半徑超級小,那麼這個星球的逃逸速度就會非常大,所以逃逸速度也是衡量天體強弱的一個參數。

圖:黑洞的質量與體積
光的速度是不變的,如果一個星球的逃逸速度大于光速,那麼光速就無法逃逸了。質量非常大,體積無限小的星球不就是黑洞的奇點嘛!

圖:史瓦西黑洞與史瓦西半徑。
當我們把光速C帶入逃逸速度公式,可以得到光是否能逃離的臨界半徑R。光離黑洞的距離大于半徑R,光就可以在黑洞踩剎車停下來之前跑掉。當進入半徑R內,光速就無法逃離了,進里面的光出不來,無法帶出黑洞中的信息,所以在這個臨界半徑里面一片黑暗,因此我們叫它黑洞,而這個臨界點叫做視界,意為視覺的界限。
引力時空彎曲
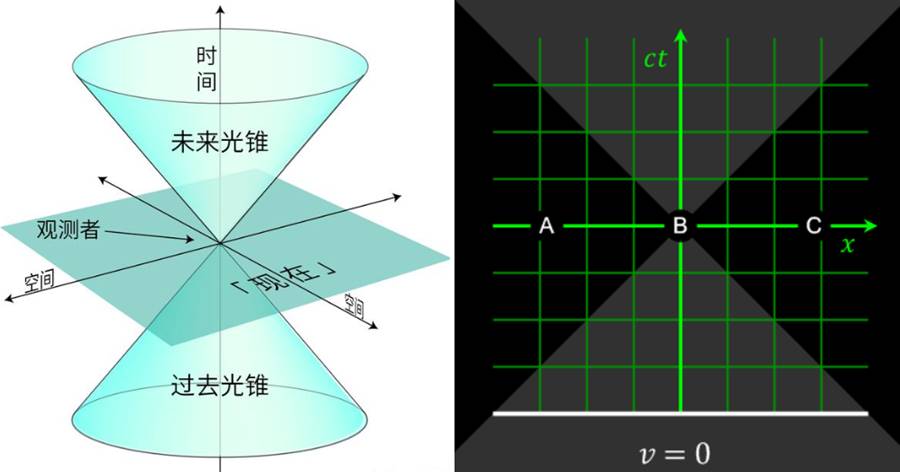
愛因斯坦在1915年發表了《廣義相對論》,他在論中指出,引力并非是力的作用,而是時空彎曲。當有質量的物體存在于時空中,那麼它周圍的時空就會因為質量的原因產生幾何變化,如下圖所示:

圖:質量物體在時空中運動,它的周圍會出現時空彎曲
拆解成二維的比較容易理解,我們隨便對時空切一刀,我們會得到一個二維的平面。當質量出現在時空中,二維平面會因為質量的影響向質量方向塌陷。

圖:為了便于理解把圖片反過來了,實際上正確的方式應該反過來看,想象成床單蓋住了小球
如果小黃球為太陽,那麼此刻在太陽形成的引力場中(扭曲的時空中)有一個作為地球的小球以一定的初速度沖了進來就會像下圖一樣:

圖:地球會圍繞著太陽一直轉
有人可能會認為小球最終會掉下去撞到大球,的確會這樣,這是因為地球存在重力,記住兩點:
小球是因為此刻地球扭曲了地球周圍的時空使小球往下掉, 請忘掉引力的作用,因為當用廣義描繪引力時,牛頓的引力就不要考慮了,這樣會重復。
當我們把這個二維實驗在大腦中還原成為三維空間,甚至是四維時空時,那就是廣義相對論的質量使時空彎曲,彎曲的時空告訴物體如何運動。

圖:物體的質量不同,時空的曲率不同
維度
時空是物體的路徑,如果時空彎曲,那麼原本走直線的小球也會跟隨彎曲。我們先以一維來說明一下,一條線,線上有只小螞蟻,小螞蟻只會在線上前進或者后退。此時如果用二維的視角來彎曲這條線,二維可以看到直線彎曲了,但對于螞蟻來說它是感受不到維度的變化的。它也只能跟著直線的變化走「曲線」,并且同一速度走曲線的時間要長。(不考慮螞蟻的維度)

我們把線換成二維的面,也讓它彎曲,從三維視角來看,就像有一個坑:

就像螞蟻只能跟著一維線走曲線,不能走紅線一樣,二維平面運動的物體也只能往坑里走,但是它自己是感覺不到它進坑了,因為二維就是一個面。

圖:螞蟻的路徑
如果有兩只螞蟻,一個從二維坑中過,一只從旁邊過,你會發現走坑用的時間比不走坑的時間要長。當二維彎曲變為三維彎曲時,我就無法簡單的畫出來了,因為需要從四維的視角去看。

圖:時空扭曲,并不完美,但意思是對的。
同理光速相同,曲率越大,光走過花的時間就越長,即曲率越大時間流速越慢。
(引力時間膨脹,這里不展開講了,不是本文的重點)
我們回顧一下一維到三維,一維螞蟻走曲線在它看來走的是直線,二維有坑,物體入坑再出來同樣會認為自己在一個平面上,走的是直線。
當三維空間扭曲的,就要靠想象力了,先說一下三維時空曲率的特性。

圖:在歐式幾何中三角形內角和為180度

圖:球形幾何中,三角形內角和大于180度,想象一下在地球的表面畫一個三角形
在球形幾何中,直線路徑為大圓,物理學中把球形幾何中過非同一直徑上的兩點所切的唯一一個大圓叫做「測地線」。
然而時空的扭曲并不是球形幾何,它的三角形內角和小于180度。

圖:時空曲率

圖:比較,中間為時空的幾何。
這些都理解了我們回到黑洞的問題,黑洞的空間極度扭曲,在視界之內的時空的測地線都指向黑洞的中心「奇點」。視界內的空間中的三角形無限逼近于一條直線,指向黑洞的角,角度幾乎為「零」。
一旦進入視界之中,所有無論你從哪個方向看去,前方都是奇點,光子并非被黑洞吸進去,它只是按著時空中的直線行進而已,并且由于時空的扭曲連回頭路的終點都是奇點,所以一旦進入黑洞的視界我們無法出來,不是不想出來,是沒有路。
光子的宿命與宇宙的宿命
那麼光最終去哪了呢?首先奇點的意義為數學上「無法解釋」的一個點,黑洞內到底有沒有奇點,這個點有多致密,目前都只是猜測,因為誰也無法進去看看再出來。但我們能肯定的是黑洞內有質量。在愛因斯坦質能等價方程告訴我們,質量只是能量的另外一種形態,所以光子并非沒有質量,只是沒有靜態質量,我們可以根據E=mc^2,推導出光子的質量m=E/c^2。

圖:一切物體的靜態質量的起點,都源于希格斯場賦予基本粒子的能,光子不受希場影響

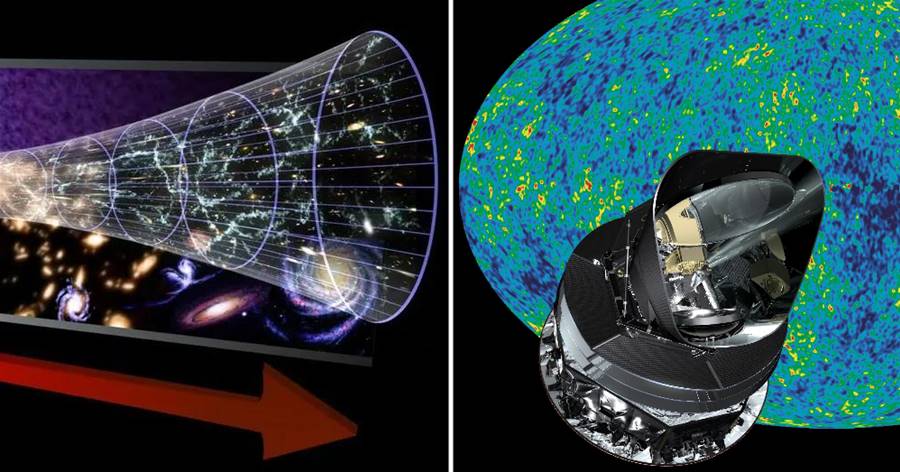
圖:黑洞蒸發
大量的光子進入黑洞之后有很大的可能性等價為黑洞的質量,畢竟能量需要守恒,哪怕是黑洞也要遵守。如果黑洞可以稱體重,隨著它吞噬大量能量與物質,它的體重肯定會增加,但是霍金說黑洞也會慢慢蒸發,隨著宇宙的演化,根據熱力學第二定律,黑洞可能成為宇宙最后的負熵保持者,直到最后一個黑洞蒸發殆盡,宇宙或許將區域平衡,時間、空間將不復存在!