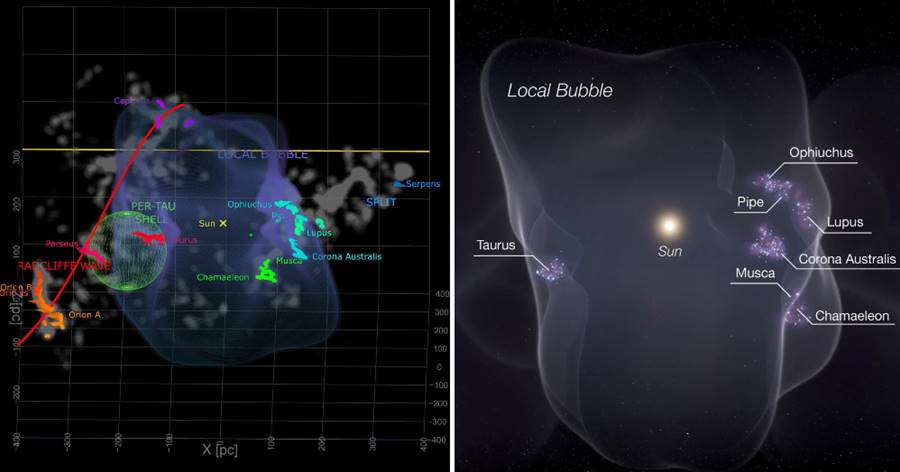
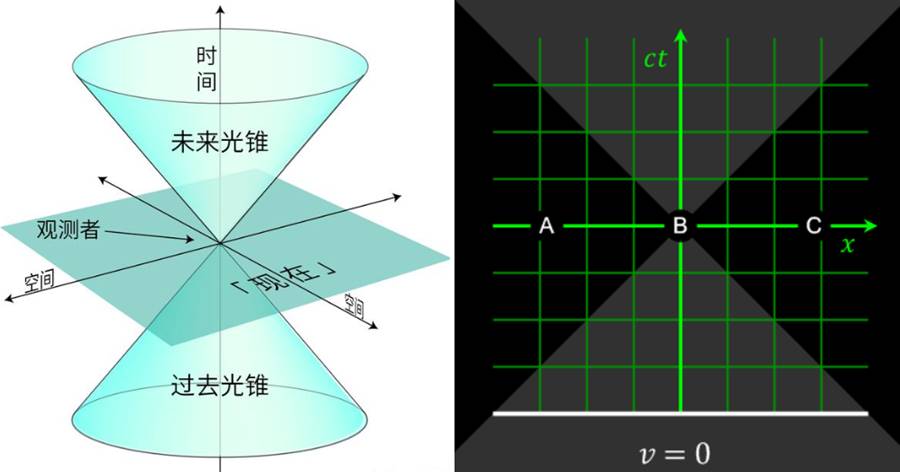
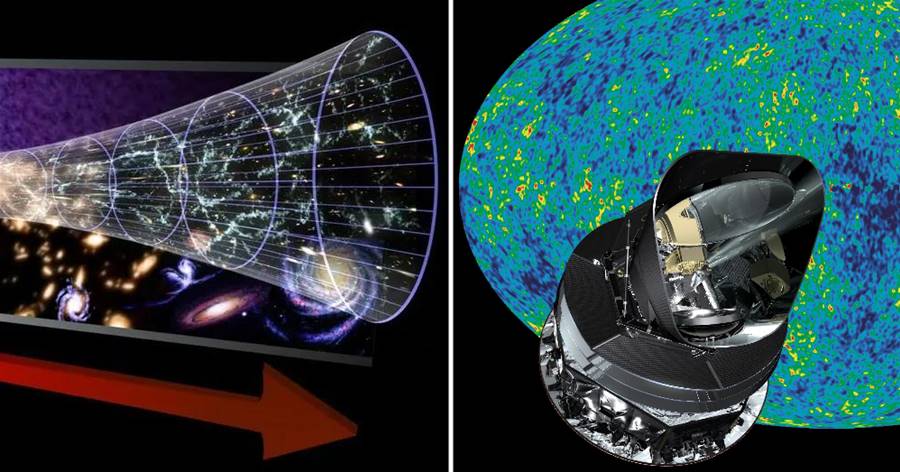
光年，并不是時間，而是距離，指的是光飛行一年的距離，大約9.46萬億公里。一光年的距離對于生活在地球上的人類來講遙不可及，但由于宇宙實在太浩瀚了，用公里這種單位描述宇宙實在不方便，所以只能用更大的單位光年，實際上即使是光年，在浩瀚宇宙面前也顯得很渺小。

光年的概念，其實一點也不難，很好理解。不過我還是需要較真一下，因為只有較真了，才能明白光的背后藏著很多奧秘：一光年指的是光飛行一年的距離，但一光年的距離真的需要光飛行一年時間嗎？

這種問題看起來有點繞嘴，也有點抬杠的味道，但其實并不是這樣的。光年確實是光飛行一年的距離，這沒有錯，但一光年的距離真的不需要光飛行一年。

該如何理解？

首先，我們需要明白一點：光飛行一年的距離是一光年，這里的「一年」時間對于我們人類來講，而不是「光的一年」！明白這點很重要。

愛因斯坦的狹義相對論告訴我們，物體隨著速度的增加，時間流逝的速度會變慢，這被稱為「時間膨脹效應」。任何具有靜質量的物體都無法達到光速，只有無限接近。如果物體的速度達到光速了，意味著物體其實已經變成光子了，不再是「物體本身」了。

擁有靜質量的物體為何不能達到光速，看看狹義相對論中的質增公式就知道了：

公式中的m是質量，m0是靜質量，V運動速度，c為光速。從公式可以看出，當V無限接近光速時，物體質量會接近無限接近無窮大，這意味著需要無窮多的能量才能推動維持物體的速度，顯然這是不可能發生的，尤其是對于有限的宇宙來講更加不可能。

狹義相對論是基于兩個假設得出的公式，其中一個重要假設就是光速不變原理，光速在任何參照系下都是光速。我們都知道，當我們說到「速度」時，必須有一個參照系，否則速度就沒有了意義。但是，光速就是如此特殊，它不需要參照系（或者在任何參照系下都是光速），光速其實是時空的內在固有秉性，嚴格來講光速并不是指光的速度，而是麥克斯韋方程組導出來的一個常數，是四維時空的固有屬性，只與真空的磁導率和介電常數有關。

一不小心說得太多了，回到正題。

明白了光速的這種特性，我們就知道對于光來講為什麼沒有時間的概念了。說白了，無論光飛行多遠的距離，對于光自身來講都是瞬間到達的，即便是穿越直徑為930億光年的可觀測宇宙，也是一瞬間就可以完成。

但在我們人類眼里，并不是這樣的，一光年的距離光仍舊需要飛行一年。這既是狹義相對論中參照系選擇不同而造成的不同結果。

這樣說不太好理解，下面就用亞光速來舉例子，就很好理解了！

如果你乘坐一艘亞光速飛船離開地球，你經歷的一年與地球上的我的一年并不是一個概念，本證時間（各自的時間）是一樣的，也就是說你體驗到的一年與我體驗到的一年長度是一樣的，這并不矛盾，因為參照系的選擇不同造成的結果，也體現了時間的相對性和同時的相對性。

也就是說，對于兩個不同的參照系來說，對同一個事件的時間觀察結果是不一樣的。

舉個例子。比鄰星距離地球大約4.3光年，如果你乘坐亞光速飛船（假設非常接近光速）飛往比鄰星，地球上的我來看，你需要大約4.3光年多一點的時間到達比鄰星，但對于飛船上的你來講，遠遠不用4.3光年。

當你亞光速飛行時，時空變化就非常明顯，尺縮效應也體現得非常明顯，地球與比鄰星（阿爾法星）之間的距離就不再是4. 3光年，會比4.3光年短，距離短多少取決于你到底有多接近光速。理論上分析，比鄰星完全有可能就在你眼前，你瞬間就可以到達比鄰星，當然前提是你必須無限接近光速飛行。

當然，也可以用速度越快所用時間就越短來詮釋，時間膨脹效應與尺縮效應是對等的，因為時間和空間本來就是有機的整體，不可分割。

這里牽扯到一個問題，類似于「雙生子佯謬」。

地球上的我眼里來看，你飛到比鄰星需要4.3年，而你感覺自己遠遠不用4.3光年，我會看到你的時鐘變慢了，并且你的一切動作都變慢了，就像電影里的慢動作播放一樣。

當然，由于速度是相對的，你看到我的效果也是一樣，你會看到我的時鐘也變慢了，我的一切動作也都變慢了。

那麼，到底誰的時間變慢了？兩者看起來有些矛盾。

其實一點也不矛盾。因為你和我處于兩個不同的參照系，我們兩人觀察到的結果都只能代表各自的參照系，無論什麼結果都不會發生矛盾，我們兩人觀察到的結果都是對的。

那麼，為何說亞光速飛行的你會變得更年輕呢？

所謂的「年輕」也是相對的，也就是說，你和我必須重新回到同一個參照系，才有資格比較誰更年輕。如果我們兩人一直處于兩個不同的參照系（永遠不返回地球），討論「誰更年輕」就沒有意義了。所以，你必須重新回到地球，然后再去比較到底誰更年輕。

如果你想返回地球，一定會經歷減速和假設的過程，這個過程其實才是真正的改變了時間，減速和加速過程讓你的時間變慢了。我地球上的我并沒有經歷減速和加速過程。

有一個公式可以計算出你的時間相對我的時間到底變慢了多少，這個公式就是：

最后強調一點，在任何參照系里，自我感覺到的時間（本證時間）都是一樣的，沒有任何區別。