看到這個題目你可能有點懵，有點繞口令的感覺。

簡單講，在我們眼里，光飛行一年的距離的確是一光年，但對于光本身來講，光飛行一光年的確不需要一年時間，嚴格來講不需要任何時間，瞬間就可以飛行一光年的距離。

兩者并不矛盾，只是參照系的選擇不同造成的不同結果。

由于光始終以光速飛行，所以，不要說一光年了，哪怕再遙遠的距離，比如說宇宙的邊緣（930億光年遠），光也會瞬間到達，不需要任何時間。

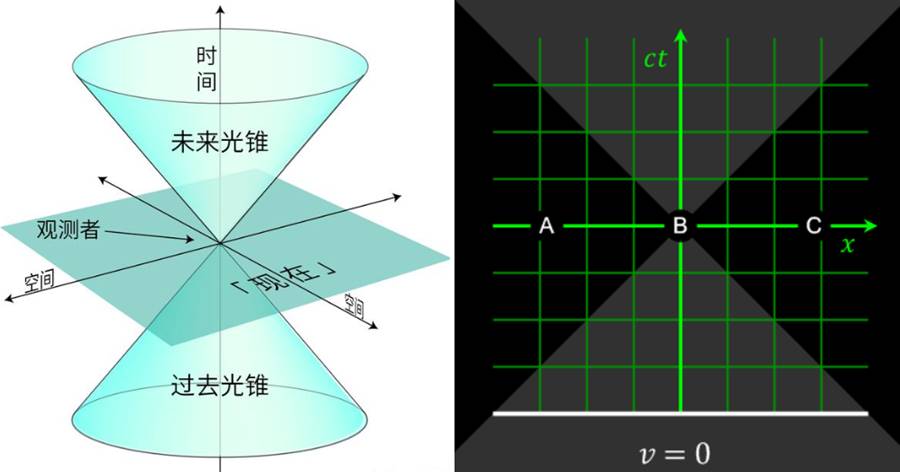
根據愛因斯坦的狹義相對論，當一個物體以亞光速飛行時，會出現明顯的時間膨脹效應（鐘慢效應）和尺縮效應。

速度越快，時間流逝的速度將越慢，當物體的速度達到光速（這時候的物體其實就變成光了），時間就靜止了，或者說沒有了時間的概念。

不過具有靜質量的物體的速度是不可能達到光速的，相對論中的質增公式已經表明了這點，速度越快，物體的質量就越大，當無限接近光速時，物體的質量就無窮大，所以不可能達到光速。

時間膨脹效應和尺縮效應公式如下：

以上公式都是基于兩個假設推導出來的：光速不變原理和相對性原理，其中光速不變原理更具顛覆性，講的是光速的絕對性，光速與其他任何速度疊加之后仍舊是光速，光速不需要任何參照系，或者說在任何參照系下光的速度保持光速不變。

在狹義相對論的理論體系下，時間和空間不再是絕對的，而是相對的，具有彈性。同時時間和空間是有機的整體，任何把時間和空間分割開來的行為都沒有意義。

所以，本質上來講，時間膨脹效應和尺縮效應是同等概念，兩者是同時發生的。

由于時間膨脹（時間變慢），飛行同等距離所用的時間自然會更少，表現出來的也是尺縮效應。當你以亞光速飛行，在我們（地球人）眼里一光年的距離，瞬間就會變短，具體變短多少取決于你接近光速的程度。

舉個例子，你乘坐一艘飛船從地球出發飛往4.3光年外的比鄰星，假設飛船的速度可以瞬間達到亞光速，在達到亞光速的瞬間，4.3光年的距離在你眼里不再是4.3光年，而會比4.3光年要小。因為亞光速飛行的飛船會出現明顯的尺縮效應。

而光的尺縮效應會達到最大，因為光始終以光速飛行，不管多遠的距離，在光的眼里（假設光有意識）都是近在咫尺。