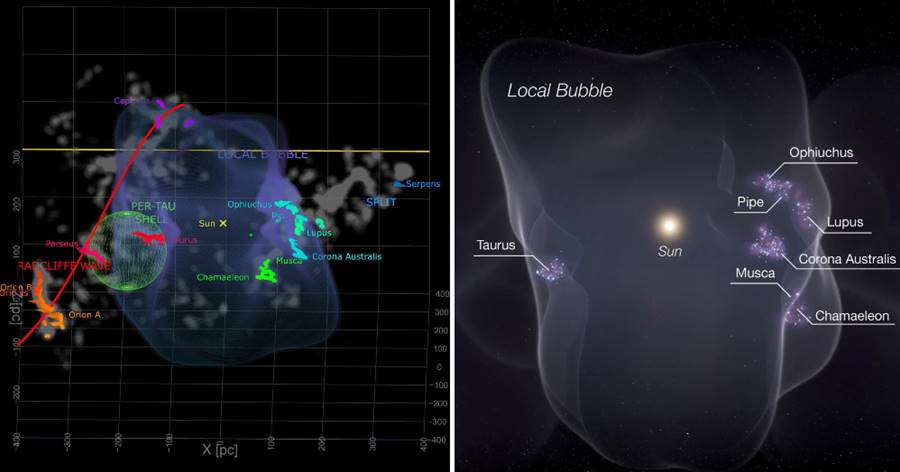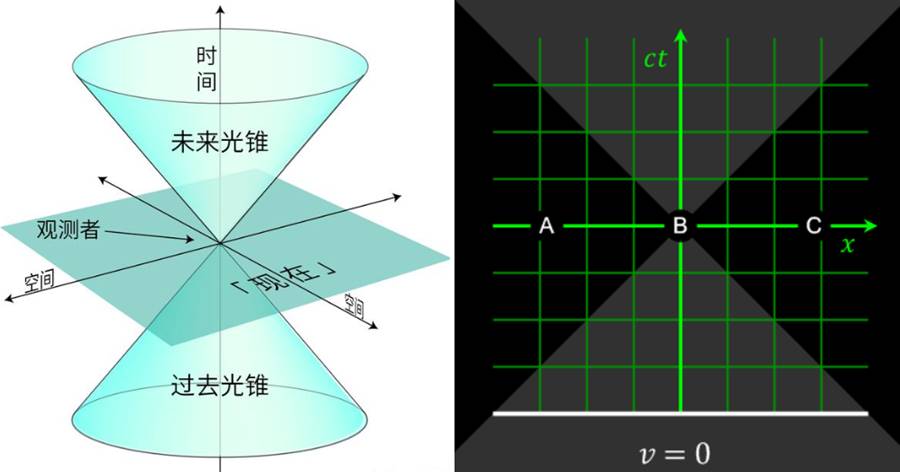
關于光速，記住一句話足以：順風的光速不會更快，逆風的光速也不會更慢，光速是恒定不變的。

光速不變

我們在來看看這個題，我們拆分一下，慢慢推進。

一束光對于一陣風（無論逆風還是順風）來說，它的速度是c，對于在地球上靜止的我們來說也是c。

一束光對于一輛高速行駛的車來說（無論順路還是不順路）來說，它的速度還是c，對于在地球上靜止的我們來說也是c。

一束光對于另外一束光（無論同向還是逆向）來說，這個結果就值得推敲了。

一般來說看到光速問題，很多人會直接祭出愛因斯坦的《狹義相對》，然后用論中洛倫茲變換直接代入計算，看起來好像so easy，然而卻忽略了一個問題。

洛倫茲變換或者說《狹義相對論》是由兩個公理推導而出的，除了光速不變，還有相對性原理。

如果說利用《狹義相對論》中的洛倫茲速度變換進行計算，還需要滿足另外一個條件，即相對性原理：相對參考系間應該遵循相同的物理定律。風和人，車和人都可以作為慣性系，然而一束光和另外一束，就值得深思了。

人為觀察者以人為觀察者來說，其中一束光的光速是c，另外一束光也是c，在人看來它們的相對速度絕對是2c，即c+c。

例如：一個光源發光，同時向四面八方釋放出光，在光源的同一直線上，同一距離相反方向放置兩個靈敏的感光設備，來測量的速度。我們得到的結果肯定是兩個c，因為光速恒定不變，于是相對速度就是2c。

（2011年，麻省理工創造了能夠捕捉光速的相機）

有人可能會說2c不是超光速了嗎？非也，這只是簡單的數學上的算術相加，是兩束光相對于靜止的人的相對速度相加，并非兩束光的相對速度。

如果要求兩束光的相對速度，那麼就要以兩束光分別為坐標系來計算。直接把光速帶入洛倫茲速度變換中，我們可以得到兩束光的相對速度為c，并非2c，然而其實c也是不對的。

因為光不能在狹義相對論中作為其中參考系，因為光不存在時間枷鎖，光速是約束時空的，這就好比你讓你一個人既當球員，又當裁判。我們先證明一下，再說結果。

（時間凝固）

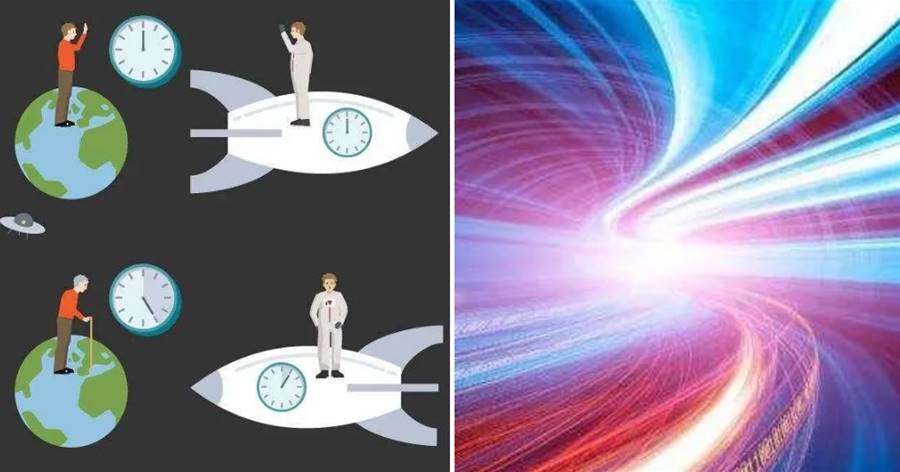
時間膨脹

愛因斯坦說時間是相對的，如果一個人拿著一個光鐘坐上宇宙飛船，在地球上的人看來光鐘并非像在地面上走的是直上直下的軌跡，而是變為了斜線。

因為光速不變原理，通過勾股定理可以得到地球時間與飛船時間的關系。

即時間膨脹公式：

由下圖可以發現，隨著飛船速度的增大，飛船上的時間與地球上的時間比值也在增大，當飛船無限趨近于光速，那麼飛船的時間將無限趨近于靜止。

（時間膨脹曲線圖）

愛因斯坦的相對高速運動，時間流速變慢就是從這里來的。

綜上所述，對于光來說它沒有時間概念，它時間是凝固的，對于我們來說太陽光花了8分鐘來到地球，對于光來說只是一瞬間的事情。它打破了時間的界限，可以在一瞬間到達宇宙中的任意位置，相對于我們來說，它才有光速這一說法。

答案

答案1：因為光相對于其他參考系為光速c，但是如果以光作為參考系，就要考慮光的本性，兩束光相對于時間是靜止的，固有時恒為0，沒有時間、也就沒有速度，所以這題無解。

答案2：順便把同向的問題也說說，盡管無法計算，但可以舉例子。太陽光為混合光，1666年牛頓把太陽光利用三棱鏡散射出多種單色光，這些單色光為同向，并且同時到達地球，所以同向為0。

反向如果非要一個答案，則為無窮，以兩個光子為例，因為光子可以在一瞬間出現在無限遠的距離，光子在不受場的干擾下，沿類光測地線運動，因為方向相反，所以無限遠加無限遠則為無窮遠，距離無限遠，時間無限小，所以答案是無窮。